トロコイド切削マクロその2 G02 G03用
さて、次はG02,G03の場合。
(Trochoid-G02G03-Path KUBOTAENGINNERING 2022/03/26) G17 G54 G40 G49 G80 G90 G21 M3 S2500 G92X0Y0Z20.000 (**********parameter**********) #3001=0.6(R) #3002=0.8(Pitch) #2011=150.(Torchoid-G01-feed) #2012=[#2011] (############G03-path############) G00Z0.1 G01Z-2.0 F50 #3101= 0 (Xa) #3102= 0(Ya) #3103= 20.(Xb) #3104= 0 (Yb) #3105= 10.(I) #3106= 0.(J) #3107=-1(G02:- G03:+) M98P7 #3101= 20.(Xa) #3102= 0(Ya) #3103= 30.(Xb) #3104= -10.(Yb) #3105= 10.(I) #3106= 0.(J) #3107= 1(G02:- G03:+) M98P7 G00Z20.000 G00X0Y0 M09 M05 M30 O7(***trochoid-G02G03***) #1206=SQRT[[#3105]**2+[#3106]**2](Rc) #1207=FUP[[0-#3105]/10000.](Xaflag +:1 0,-:0) #1208=FUP[[0-#3106]/10000.](Yaflag +:1 0,-:0) #1211=[ASIN[ROUND[[0-#3106]/#1206*1000]/1000]*#1207*#1208](ThetaA1) #1212=[[180-ASIN[ROUND[[0-#3106]/#1206*1000]/1000]]*[1-#1207]](ThetaA23) #1213=[[360+ASIN[ROUND[[0-#3106]/#1206*1000]/1000]]*#1207*[1-#1208]](ThetaA4) #1201=[#1211+#1212+#1213](ThetaA) #1220=ASIN[ROUND[[#3104-#3102-#3106]/#1206*1000]/1000] (ThetaB_BASE) #1209=FUP[[#3103-#3101-#3105]/10000.](Xbflag +:1 0,-:0) #1210=FUP[[#3104-#3102-#3106]/10000.](Ybflag +:1 0,-:0) #1221=[#1220*#1209*#1210](ThetaB1) #1222=[[180-#1220]*[1-#1209]](ThetaB23) #1223=[[360+#1220]*#1209*[1-#1210]](ThetaB4) #1202=[#1221+#1222+#1223](ThetaB) #1214=FUP[[#1206-#3002/2]/10000] (P/2<Rc:1 P/2>=Rc:0) #1203=[2*ASIN[ROUND[#3002*#1214/2/#1206*1000]/1000]+[180*ABS[#1214-1]]](ThetaPkari) #1215=[[#1202-#1201]/ABS[#1202-#1201]](a-b_DIRECTION a<b:+1 a>b:-1) #1216=[[ABS[#1202-#1201]*[#3107*#1215/2+0.5]]+[360-ABS[#1202-#1201]]*[#3107*#1215/-2+0.5]](ThetaAB) #1204=[FUP[ABS[#1216]/#1203]](n) #1205=[ABS[#1216]/#1204*#3107](STEP-ThetaP) #1505=[#1201+#1205](Theta-start) M98P8L#1204 M99 O8(****trochoid-G02G03-path****) #1231=[#3101+#3105+#1206*COS[#1505]](Xi) #1232=[#3102+#3106+#1206*SIN[#1505]](Yi) #1303=[[#1231-#3101-#3105]/#1206] (RCX) #1304=[[#1232-#3102-#3106]/#1206] (RCY) #1107=[#1303*#3001*#3107*-1] (It) #1108=[#1304*#3001*#3107*-1] (Jt) #1103=[#1231+#3107*#1303*#3001](Xsi) #1104=[#1232+#3107*#1304*#3001](Ysi) #1105=[#1231-#3107*#1303*#3001](Xei) #1106=[#1232-#3107*#1304*#3001](Yei) G01 X#1103 Y#1104 F#2011 G03 X#1105 Y#1106 I#1107 J#1108 F#2012 #1505=[#1505+#1205] M99 %
上記Gコードによるツールパスは以下
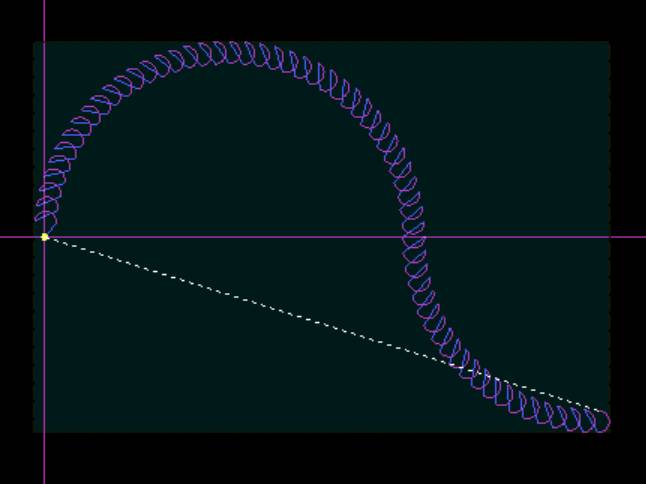
メインルーチンで始点Xa、Ya、終点Xb、Yb、中心位置I、J、G02G03判別用フラグを指定してサブルーチンO7(***trochoid-G02G03***)を呼ぶと、始点終点間角度ThetaABを計算して、トロコイドピッチPitchからステップ角度STEP-ThetaPを計算、ステップ毎にO8(****trochoid-G02G03-path****)を呼んでトロコイドのループの各座標を計算している。
ここで厄介なのが始点A、終点Bを円弧中心からの角度で表す計算。象限によって式が変わるので、条件分岐を使いたいところだが、Mach3のGコードには条件分岐はない。それでは、とそれぞれの式は全部計算しておいて、フラグパラメータをかけて該当しない象限の数値を0にして、全部足す形とした。
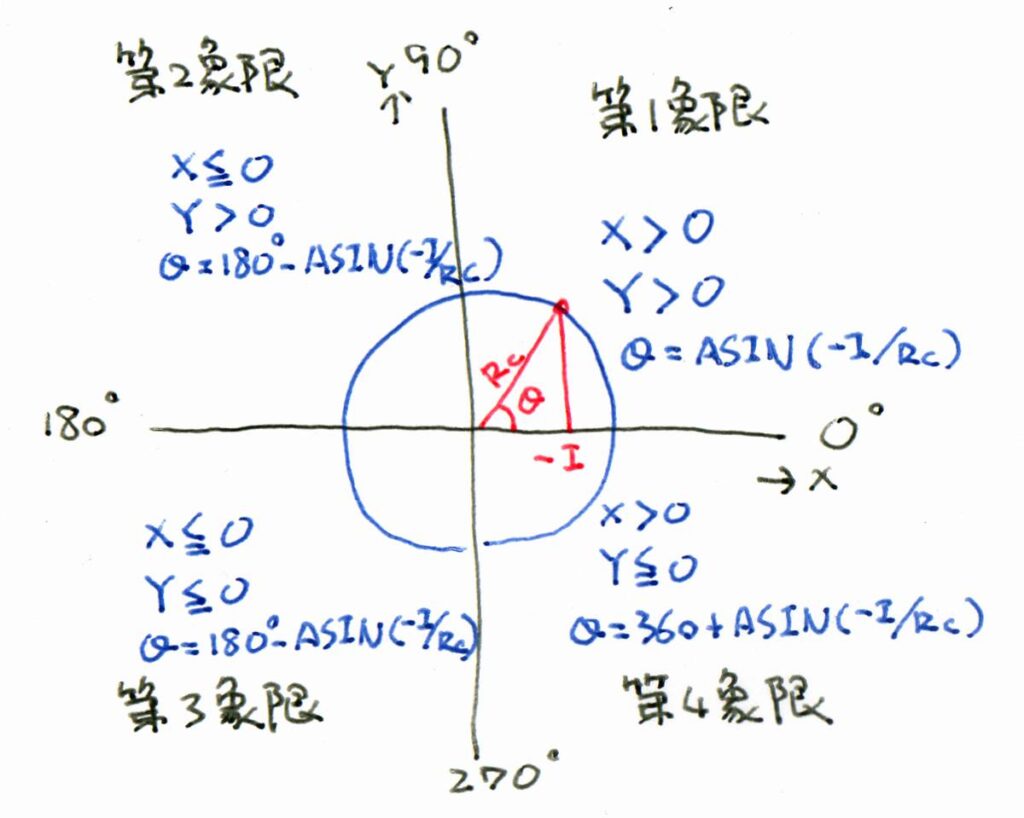
また、コード中、例えばASIN(ROUND(-I/Rc*1000)/1000)となっているのは、小数点以下4桁目を四捨五入している。これは、元ネタのGコードが I>Rcとなっていることがあり、I/Rc>1となってASINがエラーになるのを防ぐため。(これは、FreeCADのPath出力では結構頻繁に起きる。)
これで、前回のG01版と合わせて任意の溝堀りをトロコイドパスに変換することができたわけだが、パスデータをぽちぽち手打ちするのはかなりめんどくさい。
で、PYTHONでG01,G02,G03をトロコイドパスデータに変換するプログラムを作った。これは次回にでも解説する。

“トロコイド切削マクロその2 G02 G03用” に対して1件のコメントがあります。