トロコイド切削マクロその5 円弧切削時の送り速度補正

その４の条件で部品数点削ったが、どうも切り込みが深いとエンドミル刃先のチッピングがでる。ちょっと送りが高いかなーと考えてて気が付いた。

パスの半径が刃物径に対して小さいから、送り速度に刃物径補正をかけないと送りが想定より極端に高い。

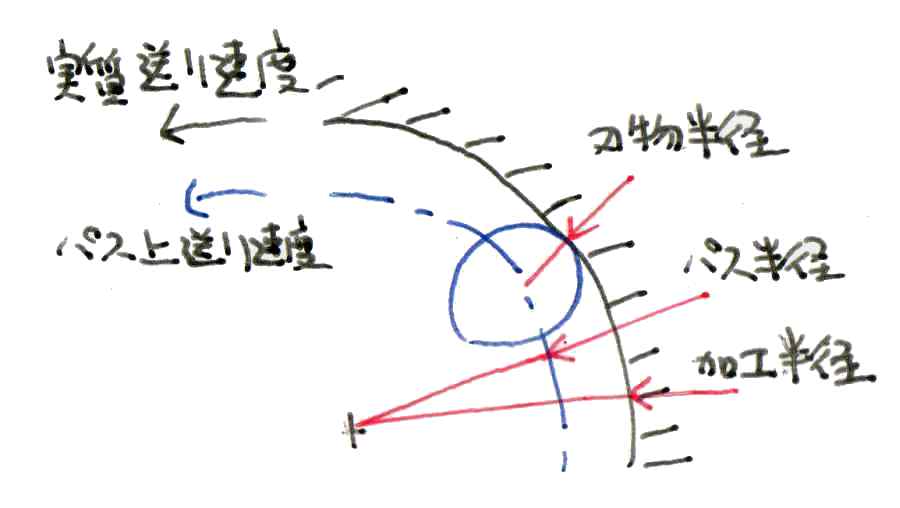
円弧切削時の実質送り速度＝パス上送り速度ｘ加工半径/加工パス半径

速度倍率＝円弧切削時の実質送り速度/パス上送り速度＝加工半径/加工パス半径

となるので、例えば工具半径3ｍｍ、加工パス半径0.4ｍｍとすると、速度倍率は（3+0.4）/0.4＝8.5倍　となる。

おっと、F300のつもりでいたら実質F2550、１刃送りなら４枚刃2500rpmとして300/2500/4＝0.03mmのつもりが実際には0.255ｍｍ、ということになる。これでは厳しかろう。

前回のマクロに刃物半径パラメータ＃3003（RCutter）を追加して

(**********trochoid parameter**********)
#3001=0.8(R) #3002=0.6(Pitch) #3003=3(RCutter for F-hosei add at VerA3)
#2011=300.(Torchoid-G01-feed) #2012=500.(Torchoid-G03-feed)

F値に速度倍率の逆数を掛けて補正した。

O5(***trochoid G01_A3***)
#1301=SQRT[[#3103-#3101]**2+[#3104-#3102]**2](L) 
#1302=[FUP[#1301/#3002]](n ) #1303=[[#3102-#3104]/#1301](RCX) #1304=[[#3103-#3101]/#1301](RCY)
#1107=[#1303*#3001](It) #1108=[#1304*#3001](Jt) #1505=0(counter Old:1 RevA2)
G01 X#3101 Y#3102 F#2011 (add at A2)
M98P6L[#1302+1](+1 AddAtA2)
G01 X#3103 Y#3104 F9999 (add at A2)
M99
O6(****trochoid-G01-path_A3****)
#1101=[#3101+[[#3103-#3101]/#1302*#1505]](Xi) #1102=[#3102+[[#3104-#3102]/#1302*#1505]](Yi)
#1103=[#1101-#1303*#3001](Xsi) #1104=[#1102-#1304*#3001](Ysi) #1105=[#1101+#1303*#3001](Xei) #1106=[#1102+#1304*#3001](Yei)
G01 X#1103 Y#1104 F#2011
G03 X#1105 Y#1106 I#1107 J#1108 F[#2012*#3001/[#3001+#3003]](F-hosei at VerA3)
G01 X#1103Y#1104 F9999 (add at A2)
#1505=[#1505+1]
M99
O7(***trochoid-G02G03_A3***)
#1206=SQRT[[#3105]**2+[#3106]**2](Rc) #1207=FUP[[0-#3105]/10000.](Xaflag +:1 0,-:0)  #1208=FUP[[0-#3106]/10000.](Yaflag +:1 0,-:0) 
#1211=[ASIN[ROUND[[0-#3106]/#1206*1000]/1000]*#1207*#1208](ThetaA1) #1212=[[180-ASIN[ROUND[[0-#3106]/#1206*1000]/1000]]*[1-#1207]](ThetaA23) #1213=[[360+ASIN[ROUND[[0-#3106]/#1206*1000]/1000]]*#1207*[1-#1208]](ThetaA4)
#1201=[#1211+#1212+#1213](ThetaA)
#1220=ASIN[ROUND[[#3104-#3102-#3106]/#1206*1000]/1000]  (ThetaB_BASE) #1209=FUP[[#3103-#3101-#3105]/10000.](Xbflag +:1 0,-:0)  #1210=FUP[[#3104-#3102-#3106]/10000.](Ybflag +:1 0,-:0)
#1221=[#1220*#1209*#1210](ThetaB1) #1222=[[180-#1220]*[1-#1209]](ThetaB23) #1223=[[360+#1220]*#1209*[1-#1210]](ThetaB4)
#1202=[#1221+#1222+#1223](ThetaB)
#1214=FUP[[#1206-#3002/2]/10000] (P/2<Rc:1 P/2>=Rc:0)
#1203=[2*ASIN[ROUND[#3002*#1214/2/#1206*1000]/1000]+[180*ABS[#1214-1]]](ThetaPkari)
#1215=[[#1202-#1201]/ABS[#1202-#1201]](a-b_DIRECTION a<b:+1 a>b:-1)
#1216=[[ABS[#1202-#1201]*[#3107*#1215/2+0.5]]+[360-ABS[#1202-#1201]]*[#3107*#1215/-2+0.5]](ThetaAB)
#1204=[FUP[ABS[#1216]/#1203]](n) 
#1205=[ABS[#1216]/#1204*#3107](STEP-ThetaP)
#1505=[#1201](Theta-start Old:#1201+#1205 RevA2)
G01 X#3101 Y#3102 F#2011 (add at A2)
M98P8L[#1204+1] (+1 AddAtA2)
G01 X#3103 Y#3104 F9999 (add at A2)
M99
O8(****trochoid-G02G03-path_A3****)
#1231=[#3101+#3105+#1206*COS[#1505]](Xi)  #1232=[#3102+#3106+#1206*SIN[#1505]](Yi)
#1303=[[#1231-#3101-#3105]/#1206]  (RCX)  #1304=[[#1232-#3102-#3106]/#1206]  (RCY)
#1107=[#1303*#3001*#3107*-1]        (It)  #1108=[#1304*#3001*#3107*-1]        (Jt)
#1103=[#1231+#3107*#1303*#3001](Xsi) #1104=[#1232+#3107*#1304*#3001](Ysi) #1105=[#1231-#3107*#1303*#3001](Xei) #1106=[#1232-#3107*#1304*#3001](Yei)
G01 X#1103 Y#1104 F#2011 
G03 X#1105 Y#1106 I#1107 J#1108 F[#2012*#3001/[#3001+#3003]](F-hosei at VerA3)
G01 X#1103Y#1104 F9999 (add at A2)
#1505=[#1505+#1205]
M99

修正したマクロ　VerA3を使って削ってみた。

加工条件は、材質：S50C　エンドミル：OSG　AE-VML6 　主軸回転数:2500rpm　パス半径R0.3　円弧ピッチP0.6　軸方向切り込みAp7.8　直線送りF300　実質円弧送りF500

前VerA2と比べると円弧部分の速度がぐっと遅くなって、チッピングは発生しなくなったようだ。切削負荷が下がった分、軸方向切り込みを増やせるようになったが、やはり遅い。パス半径R0.3　円弧ピッチP0.6　直線送りF300　実質円弧送りF500として100mm削るのに4分21秒。つまり実質F23程度。VerA2ではパス半径R0.3　円弧ピッチP0.6　直線送りF300　パス上円弧送りF300として100mm削るのに1分7秒、実質F90程度だったので、もう少し速度を上げたい。元が無理をしていたので仕方ない部分はあるが。しばらく使いながらパラメータを追い込んでみることにする。